Revenue forecasting with linear methods.
This post highlights linear regression techniques on time series data. We have some weekly sales data from a small business that is expected to have seasonal trends. A bike rental business in a major tourist city. Let’s dive into the data. Load up the required packages.
suppressPackageStartupMessages({
library(forecast)
})
Load the data, we have two columns with weekly revenue numbers from two different sources. Online and Phone; these correspond to sales online and via phone call to the business.
filename <- '~/data/BikeTours.csv'
# Read up the data file - first line is the header
d <- read.csv(filename, header = TRUE)
# Get the seller name
sellerName <- gsub("/|~.*data|.csv", "", filename)
str(d)
## 'data.frame': 220 obs. of 2 variables:
## $ Online: num 0.001 0.001 104 442 156 52 312 0.001 0.001 854 ...
## $ Phone : num 0.001 0.001 0.001 0.001 44.5 0.001 0.001 141 0.001 0.001 ...
The weekly revenue for BikeTours
Timeseries
Let start by creating a timeseries object using the ts() function and has the signature ts(vector, start=,end=,frequency) where start and end are times of the first and last observation and frequency is the number of observations per unit time (1=annual, 4=quarterly, 12=monthly).
In our case we have weekly data, therefore we will set our frequncy to 52.
d_ts <- ts(d, start = c(2012,1), frequency = 52)
summary(d_ts)
## Online Phone
## Min. : 0.001 Min. : 0.001
## 1st Qu.: 211.000 1st Qu.: 0.001
## Median :1824.500 Median : 191.500
## Mean :1959.751 Mean : 333.967
## 3rd Qu.:3112.500 3rd Qu.: 571.875
## Max. :8505.000 Max. :1733.000
Online and Phone revenue
Let’s look at the weekly sales split out by mode of purchase Online vs Phone. Online sales are the primary component of sales. For the next few sections we will focus on the Online component. The same analysis and forecast can be done for the Phone component.
title <- paste(" Seasonal decompsition for ", sellerName)
ts.plot(d_ts, gpars = list(col=c("tomato", "magenta"), lwd=2, ylab="Gross Sales", xlab="year", main = title))
legend('topleft' ,legend=c("Online", "Phone"), lty=1, col=c("tomato", "magenta"), bty='n', cex=.75)
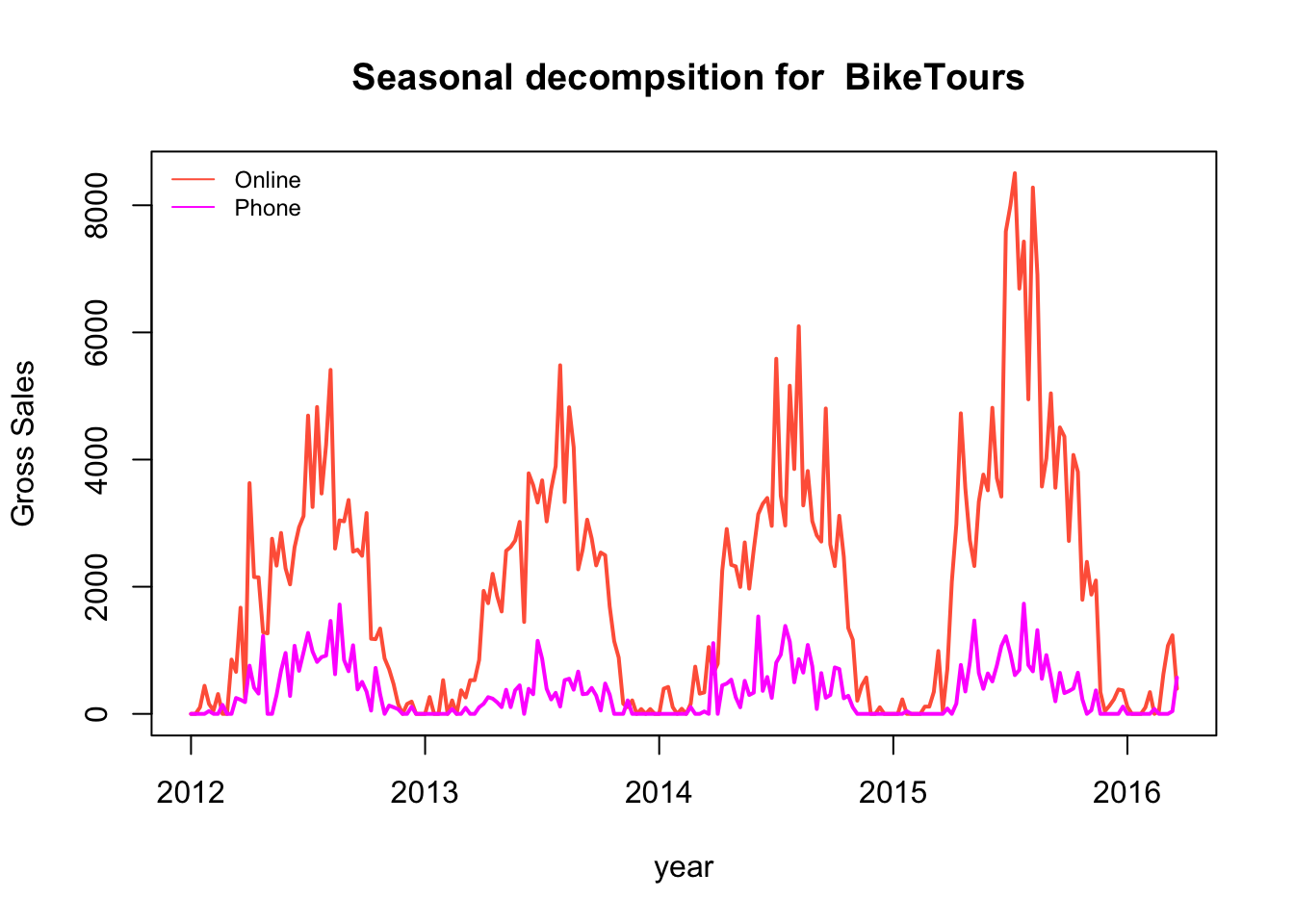
Online Revenue
Seasonal component extraction.
When a time series varies according to a periodic component, we can extract the periodicty using classical statistical methods. The stl() function in core R uses loess to effectively take the means of each period. The seasonal component is removed and the remainder is smoothed to find the trend. The sales are clearly seasonal with peaks in the middle of the year starting near spring break and ending near thanksgiving.
Weekly revenue with the seasonal component extracted
d_online <- d$Online
d_ts_online <- ts(d_online, start = c(2012,1), frequency = params$freq)
d_ts_comp_online <- stl(d_ts_online, s.window = "period", robust = TRUE)
plot(d_ts_comp_online, main = title)
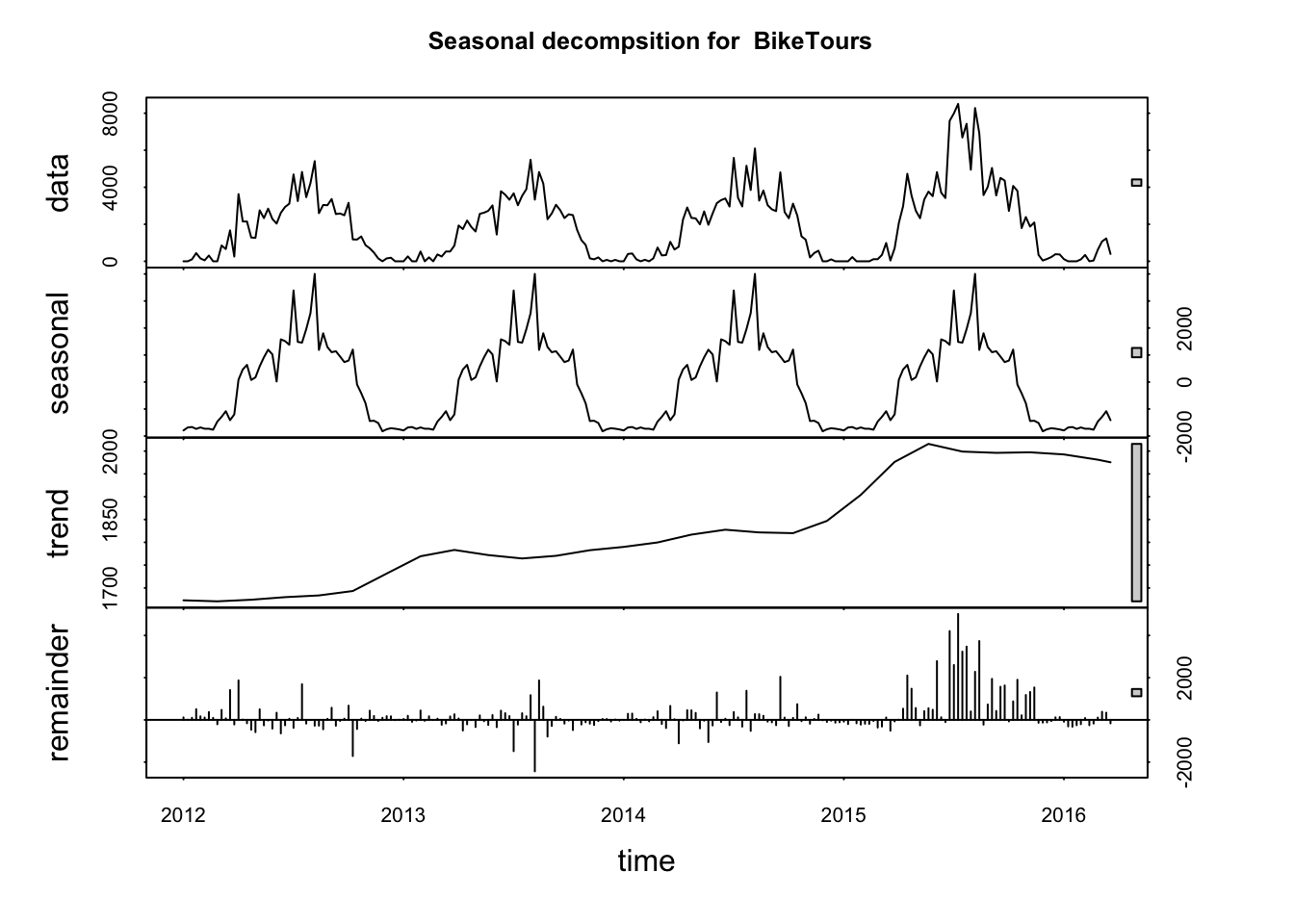
Let’s combine this into a single plot. We have also extracted the seasonally adjusted numbers to show the actual variations and trends.
plot(d_ts_online, ylab="Gross Revenue", main = "Online gross revenue with trend and seasonal parts")
lines(d_ts_comp_online$time.series[,2], col="tomato")
lines(seasadj(d_ts_comp_online), col="green")
lines(d_ts_comp_online$time.series[,1], col="blue")
legend('topleft' ,legend=c("Actual", "trend", "seasonal adj", "seasonal"), lty=1, col=c("black", "tomato", "green", "blue"), bty='n', cex=.75)
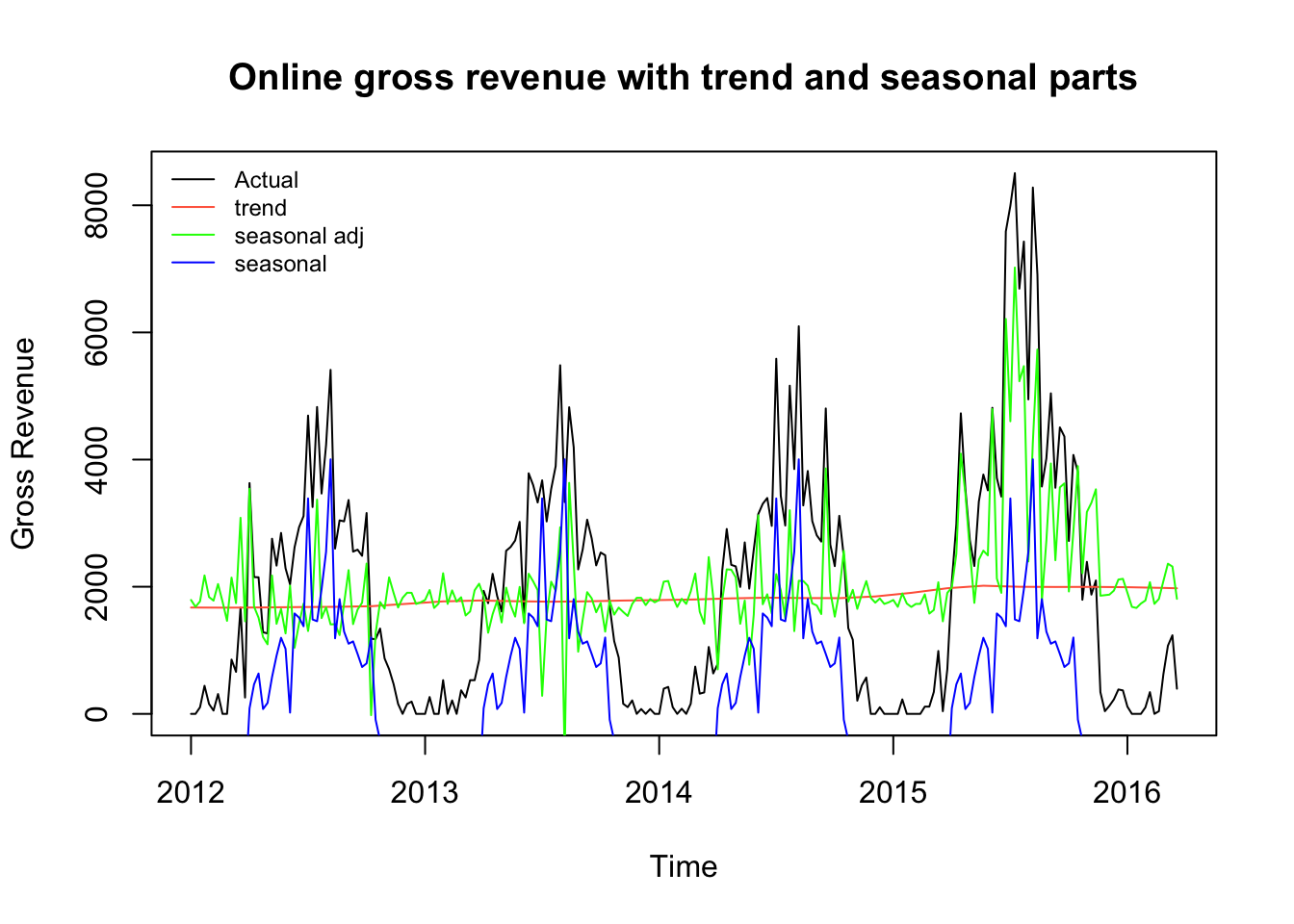
Forecast using linear regression
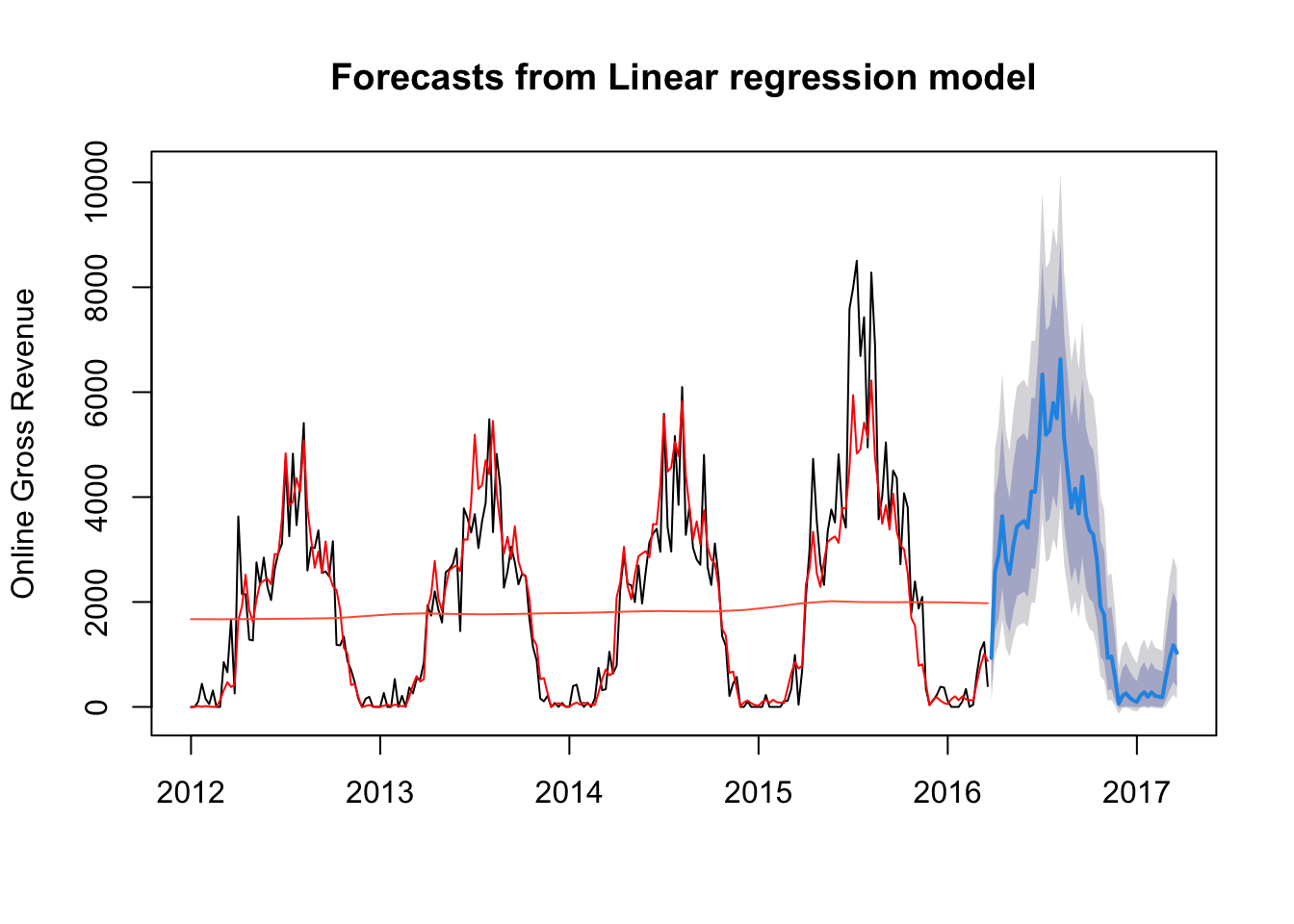
This is the forecast for revenue taking seasonality into account. The function tslm() is the linear regression version for time series data.
Note the red line shows the model’s predicted numbers.
f_online<-tslm(d_ts_online ~ trend + season, lambda = 0.5)
ff_online <- forecast(f_online, h=params$freq)
plot(ff_online, ylab="Online Gross Revenue")
lines(fitted(ff_online), col="red")
lines(d_ts_comp_online$time.series[,2], col="tomato")
Forecast using ARIMA models
Let’s also use the [ARIMA](https://en.wikipedia.org/wiki/Autoregressive_integrated_moving_average Wikipedia) model to get a forecast. Note that the D=1 parameter forces the model to take seasonality into account.
f_online_arima <-auto.arima(d_ts_online, lambda = 0.5, D=1)
ff_online_arima <- forecast(f_online_arima, h=params$freq)
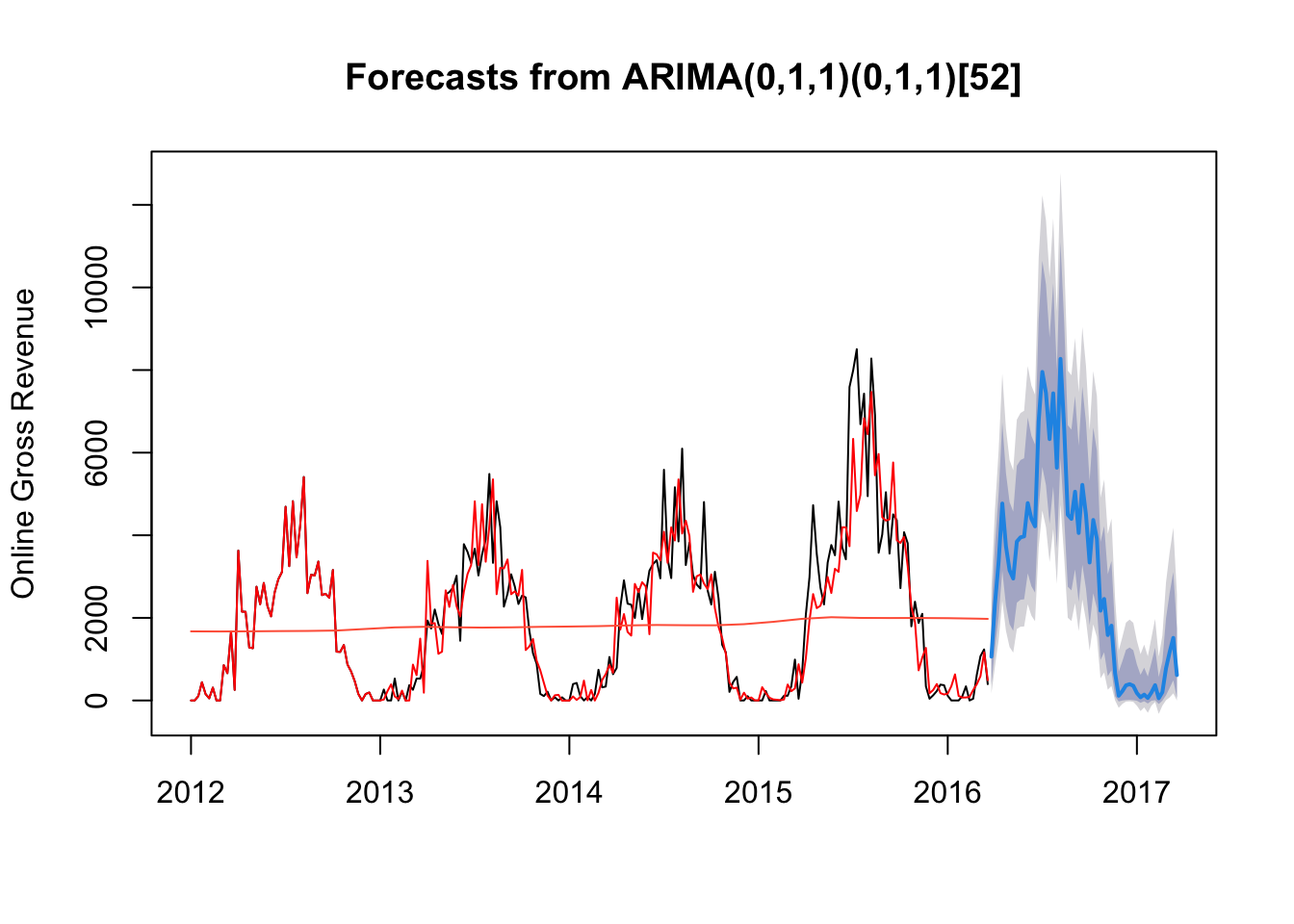
plot(ff_online_arima, ylab="Online Gross Revenue")
lines(fitted(ff_online_arima), col="red")
lines(d_ts_comp_online$time.series[,2], col="tomato")
Residuals
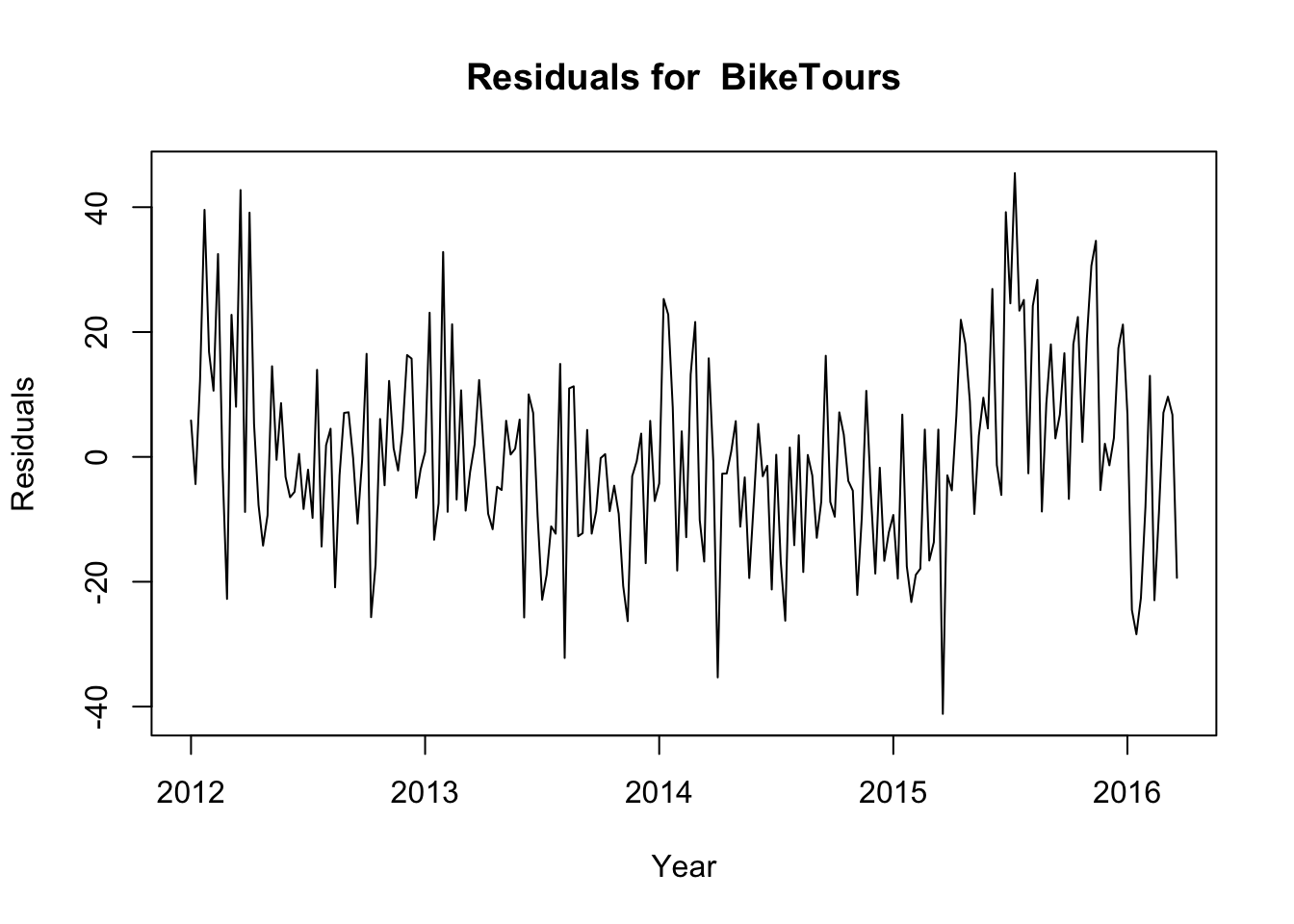
The residuals - the difference between the actual and predicted values back fitted. Low numbers are indicative of a good fit. A 0 mean is indicative of an unbiased forecast.
res <- residuals(ff_online)
plot(res, ylab="Residuals",xlab="Year", main = paste("Residuals for ", sellerName) )
summary(res)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -41.166 -9.406 -1.330 0.000 8.180 45.450
Autocorrelation
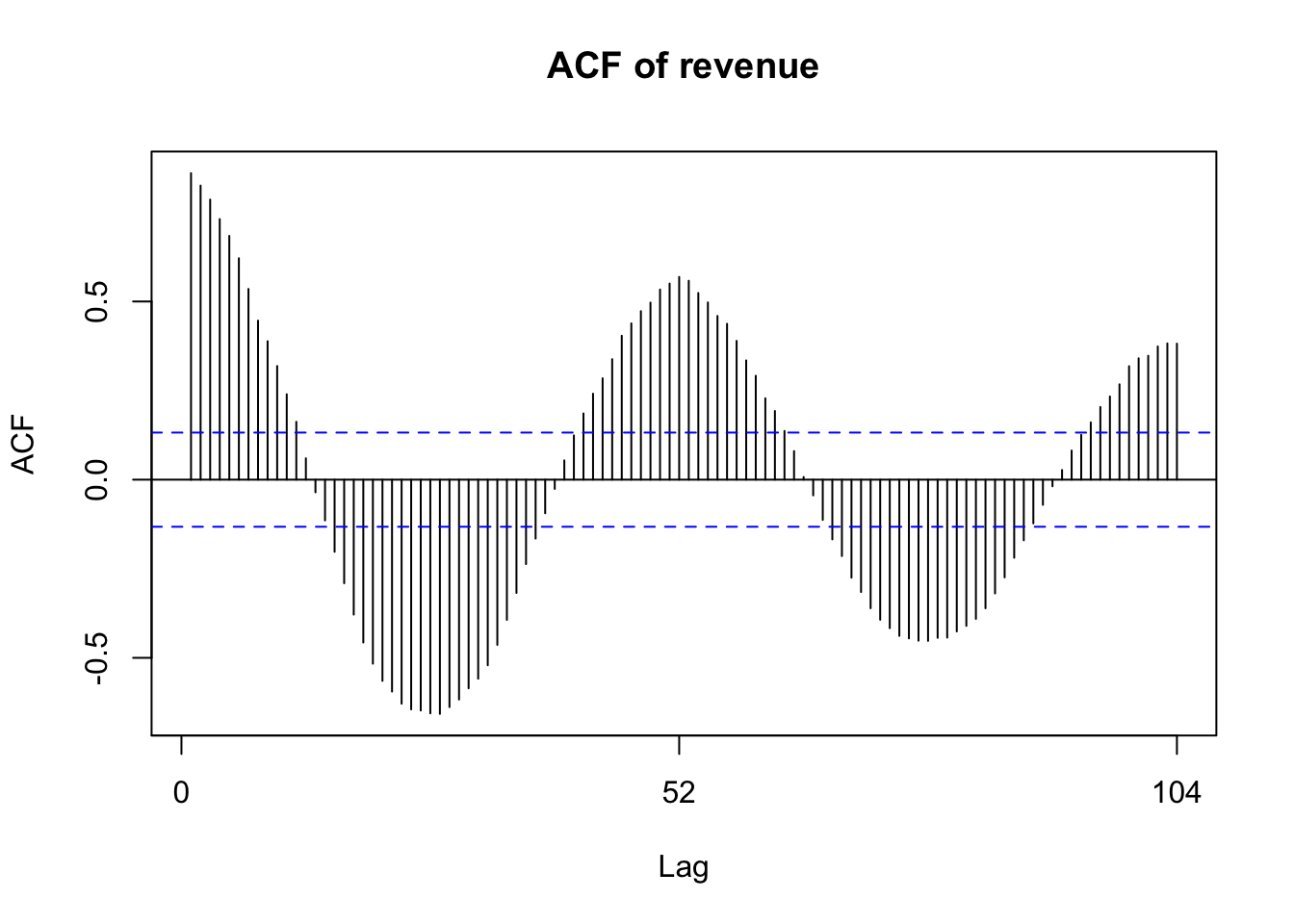
The autocorrelation shows the correlation between seasonal data, peaks show positive correlation at the marked intervals. ( 52 weeks, so yearly correlation is statistically signficant - i.e. above the blue line)
Acf(d_ts_online , main="ACF of revenue")
This is the weekly revenue prediction using this model
ff_online
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 2016.231 932.32319 318.4182798 1868.2845 122.377409 2500.5504
## 2016.250 2578.50032 1450.7906998 4028.2664 980.153309 4935.1287
## 2016.269 2899.35343 1693.8126535 4426.9506 1181.579368 5375.4089
## 2016.288 3636.01505 2266.6825172 5327.4040 1666.912767 6363.3987
## 2016.308 2811.32749 1626.6914914 4318.0199 1125.630506 5255.3059
## 2016.327 2534.91901 1418.1468035 3973.7476 953.354775 4874.7646
## 2016.346 3060.37223 1817.3972106 4625.4037 1285.157659 5593.8682
## 2016.365 3436.28453 2109.5778794 5085.0476 1532.589002 6098.2615
## 2016.385 3496.85664 2157.0949601 5158.6747 1573.128986 6178.8657
## 2016.404 3544.38422 2194.4579606 5216.3669 1605.059651 6241.9902
## 2016.423 3417.33077 2094.7327927 5061.9852 1519.939747 6073.0032
## 2016.442 4106.06462 2640.8182622 5893.3674 1989.788563 6980.6221
## 2016.462 4100.72397 2636.5355784 5886.9688 1986.071299 6973.6580
## 2016.481 4906.16729 3289.5213509 6844.8697 2557.578032 8013.0379
## 2016.500 6338.84958 4479.2505450 8520.5050 3617.463974 9818.5166
## 2016.519 5186.98677 3520.1734058 7175.8566 2761.418733 8370.8362
## 2016.538 5270.49922 3589.0301382 7274.0247 2822.442901 8476.8369
## 2016.558 5797.34323 4025.9782912 7890.7646 3211.347336 9141.6205
## 2016.577 5501.54321 3780.1223019 7545.0205 2992.183310 8769.1845
## 2016.596 6625.44928 4720.6757023 8852.2793 3834.746161 10174.4338
## 2016.615 5116.51520 3462.1610316 7092.9258 2710.065021 8281.2468
## 2016.635 4448.71331 2916.9705965 6302.5125 2230.402750 7425.3053
## 2016.654 3794.23255 2391.9585078 5518.5630 1774.583579 6572.1629
## 2016.673 4162.58023 2686.1801445 5961.0367 2029.189479 7054.2524
## 2016.692 3681.91917 2302.9566493 5382.9381 1698.040275 6424.0795
## 2016.712 4390.17215 2869.6040100 6232.7967 2189.008275 7349.6174
## 2016.731 3632.94408 2264.2579505 5323.6866 1664.833664 6359.3359
## 2016.750 3369.14148 2057.0412819 5003.2981 1487.858639 6008.7057
## 2016.769 3282.84745 1989.7352906 4898.0160 1430.700569 5893.2757
## 2016.788 2810.32651 1625.9300943 4316.7793 1124.997152 5253.9373
## 2016.808 1909.04629 961.1825996 3178.9664 586.661624 3989.7123
## 2016.827 1755.20285 852.9584196 2979.5037 502.818088 3765.8690
## 2016.846 931.63616 318.0168235 1867.3119 122.128578 2499.4251
## 2016.865 962.29862 336.0346946 1910.6190 133.388706 2549.4899
## 2016.885 560.41274 120.6339549 1322.2479 17.652625 1861.4542
## 2016.904 63.23344 -22.4462142 426.0771 -132.700951 752.0473
## 2016.923 208.05583 3.0083216 735.1598 -25.476195 1148.9169
## 2016.942 259.64447 11.7223916 829.6230 -11.276489 1266.2938
## 2016.962 179.62121 0.5077909 680.7911 -36.835817 1080.6880
## 2016.981 123.96826 -2.4198465 567.5731 -69.512770 936.7052
## 2017.000 94.68002 -7.5661760 493.3463 -88.755270 834.1545
## 2017.019 219.76105 5.4910801 745.5834 -18.723170 1154.3487
## 2017.038 280.90078 18.3103595 855.0436 -5.718185 1289.6331
## 2017.058 191.89206 1.8809485 693.4556 -28.077880 1089.2560
## 2017.077 279.04190 17.8380613 851.7982 -5.986930 1285.6466
## 2017.096 210.92247 4.1703189 729.2271 -21.420211 1133.9745
## 2017.115 196.93559 2.4097589 703.0138 -26.193857 1101.2271
## 2017.135 183.21704 1.1124655 676.8741 -31.534946 1068.4489
## 2017.154 577.11718 133.2230499 1332.5637 23.735368 1864.0487
## 2017.173 927.77902 323.2239800 1843.8865 127.873075 2461.2347
## 2017.192 1177.07497 476.4394082 2189.2630 229.739463 2857.9602
## 2017.212 1031.06060 385.3014920 1988.3721 167.929587 2627.7414